物理 必修一
第一章 运动的描述
1.1 质点 参考系
物体和质点
- 定义:在某些情况下,可以忽略物体的大小 和形状,把它简化为一个具有质量的点,这样的点叫作质点。
- 条件:物体的大小和形状对所要研究的问题没有影响或者影响很小。
- 物理意义:质点是一个理想化的物理模型 ,实际上并不存在
参考系
- 定义:描述一个物体的运动时,选来作为参考的物体 叫做参考系。
- 选取原则:
- 任意性原则:参考系的选取是任意的,选择不同的参考系描述同一物体的运动,其结果可能不同。
- 方便性原则:选择参考系时,应以观察方便和运动的描述尽可能简单为原则。在研究地面上的问题时,通常选择地面或相对地面静止的物体作为参考系。
- 同一性原则:当比较两个物体的运动情况时,必须选择同一个参考系。
1.2 时间 位移
时刻和时间间隔
| 时刻 | 时间间隔 | |
| 物理意义 | 某一瞬间 | 某一时间(段) |
| 在时间轴上的表示 | 时间轴上的点表示时刻 | 时间轴上的一段线段表示时间间隔 |
| 对应的物理量 | 位置、瞬时速度、瞬时加速度 | 位移、速度的变化量、平均速度 |
| 联系 | $\Delta t = t_2 - t_1$ | |
| 示意图 | 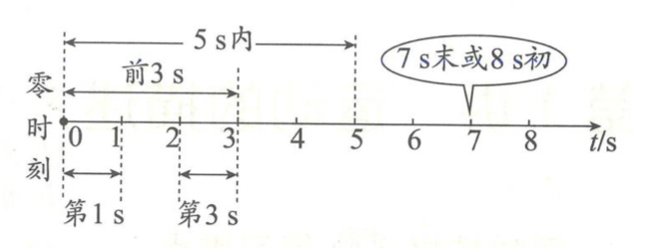 |
|
位移和路程
- 路程:物体运动轨迹的长度。
- 位移:描述物体位置变化的物理量,可用由初位置指向末位置的有向线段表示。线段的长度表示位移的大小,箭头的指向表示位移的方向。
- 知识点:x-t图像
从A到B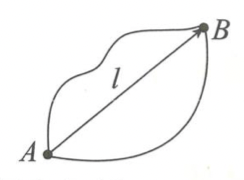
矢量和标量
- 矢量:既有大小又有方向的物理量。运算遵循平行四边形 定则(或三角形定则)。矢量可用有向线段表示,线段的长度表示矢量的大小,箭头指向表示矢量的方向。
- 标量:只有大小没有方向的物理量。运算遵循算术运算法则。
- 矢量和标量的根本区别是运算法则不同。
直线运动的位移
-
直线运动的位移大小:做直线运动的物体,它的初位置位,末位置为,则物体的位移。
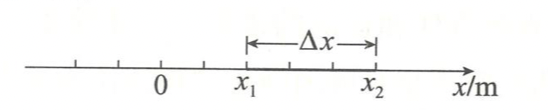
-
直线运动的位移方向:若两坐标之差为正,则位移的方向指向x轴的正方向;若两坐标标之差为负,则位移方向指向x轴的负方向。
位移-时间图像
-
定义:在直角坐标系中选时刻t为横轴,选位置x为纵轴,其上的图线就是位置-时间图像。如果将物体运动的初始位置选作位置图标原点,则位置与位移大小相等,位置-时间图像就成为位移-时间图像,又称图像。
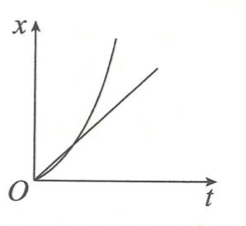
-
对图像的理解
- 图像不是物体的运动轨迹。
- 图像反映了做直线运动的物体的位移随时间变化的规律。
- 图像只能描述物体做直线运动的情况。
- 图像中的交点表示物体相遇。
- 图像的斜率表示速度。
1.3 位置变化快慢的描述-速度
速度
- 概念:物理学中用位移与发生这段位移所用的时间之比表示物体运动的快慢。
- 定义:
- 单位:在国际单位制中,速度单位是或。
- 矢量性:速度是矢量,既有大小,又有方向。速度的方向与位移方向相同。
平均速度和瞬时速度
| 平均速度 | 瞬时速度 | |
| 定义 | 物体的位移$\Delta x$跟发生这段位移所用的时间$\Delta t$的比值$\overline{v}=\dfrac{\Delta x}{\Delta t}$ | 物体在某一时刻或某一位置的速度,即$v=\dfrac{\Delta x}{\Delta t}\left(\Delta t \to 0\right)$ |
| 方向 | 与位移同向,与某时刻的运动方向不一定相同 | 沿运动轨迹的切线方向,与某时刻的运动方向相同 |
| 物理意义 | 表示物体在某段时间,某段位移内运动的平均快慢程度 | 精确到描述物体在某一位置或某一时刻运动的快慢 |
| 对应关系 | 与一段位移(时间)相呼应,是过程量 | 与某一时刻(位置)相对应,是状态量 |
| 联系 | 匀速直线运动中,平均速度等于瞬时速度,瞬时速度是极短时间内的平均速度 | |
平均速率
- 定义:,是标量。
- 注意:瞬时速度的大小叫做速率,也是标量。
速度-时间图像
- 定义:以时间为横轴、速度为纵轴,坐标系中的图像即为速度-时间图像或图像。
1.4 速度变化快慢的描述-加速度
加速度
- 定义:加速度为速度的变化量与发生这一变化所用的时间之比,通常用表示。
- 公式:。单位或,读作米每二次方秒。
- 矢量性:加速度是矢量,加速度的方向与速度的变化量()的方向相同。
- 物理意义:描述物体速度变化快慢的物理量。
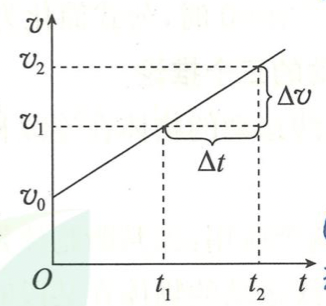
从图像看加速度
-
图线斜率的大小表示加速度的大小。
-
图线斜率的正负表示加速度的方向。
第二章 匀变速直线运动的研究
2.1 匀变速直线运动的速度与时间的关系
匀变速直线运动
- 定义:沿着一条直线,且加速度不变的运动。
- 特点:在任意相等的时间内,速度的变化量都相等,即恒定。
- 匀加速直线运动:速度随时间均匀增大,与同向。
- 匀减速直线运动:速度随时间均匀减小,与反向。
速度与时间的关系
- 公式:
- 当时,,此时物体做匀速直线运动。
- 当时,,此时物体由静止开始做匀变速直线运动。
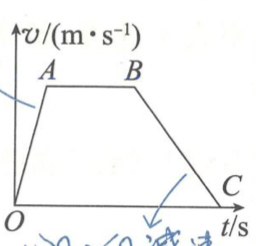
匀变速直线运动的图像
- 纵轴截距:表示初速度。
- 斜率:斜率大小表示加速度的大小,正负表示加速度的方向。
- 面积:图线与轴所围面积表示位移大小,轴下方表示沿负方向。
2.2 匀变速直线运动的位移与时间的关系
匀速直线运动的位移
- 公式:。
匀变速直线运动的位移
- 公式:。
- 如果初速度时,位移公式可以写为,此时位移与时间的二次方成正比。
2.3 匀变速直线运动的速度与位移的关系
速度与位移的关系
- 公式:
- 注意:该公式仅适用于匀变速直线运动。
匀变速直线运动的三个推论
- 做匀变速直线运动的物体在连续相等的时间内的位移之差为一恒定值,即。
- 做匀变速直线运动的物体在某段时间中间时刻的瞬时速度等于这段时间内的平均速度,即。
- 做匀变速直线运动的物体在某段位移中间位置的瞬时速度,且无论是匀加速直线运动还是匀减速直线运动,均有
初速度为0的匀加速直线运动的规律
-
末、末、末、···速度之比为:
-
内、内、内、···位移之比为:
-
第1个内、第2个内、第3个内、···位移之比为:
-
从静止开始通过连续相等的位移所用时间之比为:
2.4 自由落体运动和竖直上抛运动
自由落体运动
- 定义:物体只在重力作用下从静止开始下落的运动。
- 条件:初速度为零且只受重力作用。
- 实质:自由落体运动是初速度、加速度的匀加速直线运动。
自由落体加速度
- 定义:在同一地点,一切物体自由下落的加速度都相同,这个加速度叫作自由落体加速度,也叫作重力加速度,通常用表示。
- 方向:竖直向下。
- 大小:随高度和纬度的变化而变化,但是变化不大,在计算中,一般取或。
自由落体运动的规律
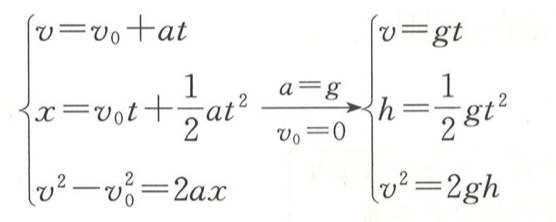
竖直上抛运动
- 定义:将物体以一定的初速度竖直向上抛出,物体只在重力作用下所做的运动叫作竖直上抛运动。
- 特点:具有一个竖直向上的初速度,运动过程只受重力作用,加速度恒为重力加速度。
- 性质:初速度不为零的匀变速直线运动。
- 规律:
- 取初速度方向为正方向,加速度。
- 运动学方程:

- 上升时间:
- 最大上升高度:


